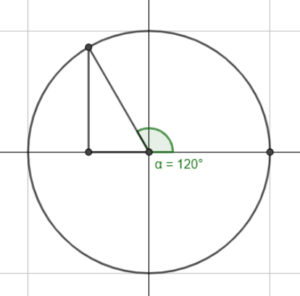
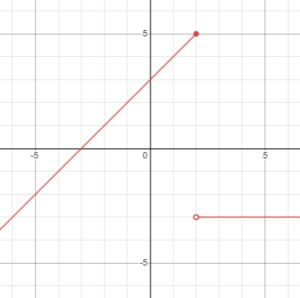
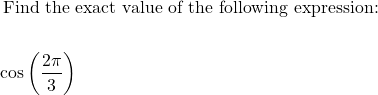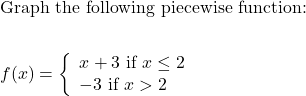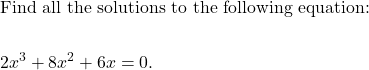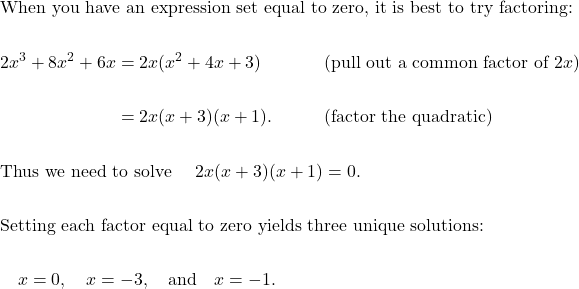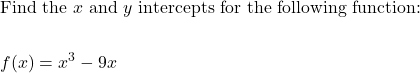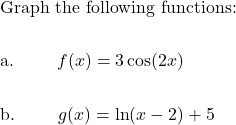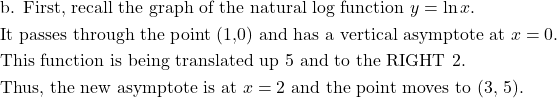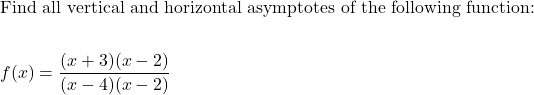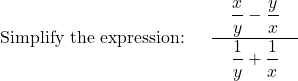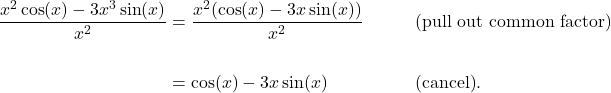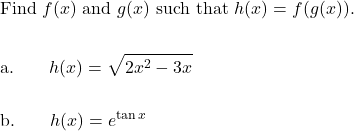MAT 126 Course Prep

Note: This page contains LaTeX markup to display mathematical notation.

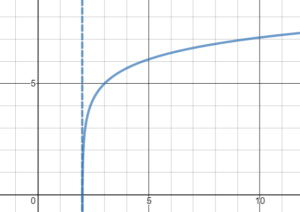
This collection of problems is meant to provide practice for a range of skills needed for MAT 126. Read and attempt each problem first; if you aren’t sure how to start a problem, explore the resources on the right to refresh your memory and try again. A drop-down button is found beneath each problem for you to compare both your logic and final answers. Keep track of the skills you aren’t comfortable with, and reacquaint yourself with them so you’re fully prepared for the topics you’ll grapple with soon. Get help in the Math Lab.  Return to the Course Prep page.

Problem 01\begin{aligned}&\text{ Find the exact value of the following expression: }\\\\&\cos \left(\dfrac{2 \pi}{3}\right)\end{aligned}
Click here to show solution.

Solution:

\begin{aligned}&\text{By definition, } \: \cos(\theta) \text{ is the } x \text{-coordinate of the point on the unit circle determined by } \: \theta. \\\\&\text{Note: The unit circle is a circle of radius 1 centered at the origin.} \\\\&\text{To determine that point, we need to draw an angle of size } \theta \text{ in standard position.} \\\\&\text{Note: Standard position means we start from the positive x-axis and rotate counter-clockwise by } \theta. \\\\&\text{The angle } \theta = \dfrac{2\pi}{3} \text{ is given in radians, and can be converted to } 120^{\circ}. \\\\&\text{Note: Any angle in radians can be converted to degrees by multiplying by } \dfrac{180^{\circ}}{\pi}.\end{aligned}

\begin{aligned}&\text{To get the } x \text{-coordinate of the point, draw the right triangle as shown above.} \\\\&\text{Notice that this is a } 30^{\circ}\text{-}60^{\circ}\text{-}90^{\circ} \text{ triangle with hypotenuse 1.} \\\\&\text{This means that the shorter leg (the bottom side of the triangle) must have length } \dfrac{1}{2}. \\\\&\text{The point on the circle is in the second quadrant, so the x-coordinate is } -\dfrac{1}{2}. \\\\&\text{Thus, } \cos \left(\dfrac{2 \pi}{3}\right) =-\dfrac{1}{2}.\end{aligned}

Need Help ?

Evaluating Trig Functions

Problem 02\begin{aligned}&\text{Graph the following piecewise function: }\\\\&f(x)=\left\{\begin{array}{l}x+3 \text { if } x \leq 2 \\-3 \text { if } x>2\end{array}\right.\end{aligned} 
Click here to show solution.

Solution:

\begin{aligned}&\text{Graph the linear function } y=x+3 \text{ when x is less than 2.}\\\\&\text{Graph the horizontal line } y=-3 \text{ when x is greater than 2.}\\\\&\text{Because of the } \leq \text{ sign, } f(2) = 2 + 3 = 5, \text{ so we place a closed circle at the point (2, 5).}\\\\&\text{Because of the } > \text{ sign, we place an open circle at the point (2, -3).}\\\\\end{aligned}

Need Help ?

Graphing Piecewise Functions

Problem 03\text {Find and simplify } \quad \dfrac{f(x+h)-f(x)}{h} \quad \text { given } \quad f(x)=-3 x^{2}-5. 
Click here to show solution.

Solution:

\begin{aligned}\dfrac{f(x+h)-f(x)}h&= \dfrac{-3 (x+h)^{2}-5-(-3 x^{2}-5)}{h} &&\qquad\text{(plug into the function)}\\\\&= \dfrac{-3 (x+h)^{2}-5+3 x^{2}+5}{h} &&\qquad\text{(distribute the -1)} \\\\&= \dfrac{-3 (x+h)^{2}+3 x^{2}}{h} &&\qquad\text{(simplify)} \\\\&= \dfrac{-3 (x^{2} +2xh +h^{2}) +3 x^{2}}{h} &&\qquad\text{(expand the squared binomial)}\\\\&= \dfrac{-3 x^{2} -6xh -3h^{2} +3 x^{2}}{h} &&\qquad\text{(distribute the -3)}\\\\&= \dfrac{-6xh -3h^{2} }{h} &&\qquad\text{(cancel the } 3x^{2} \text{)}\\\\&= \dfrac{h \; (-6x -3h) }{h} &&\qquad\text{(pull out a common factor of } h \text{)}\\\\&= -6x - 3h &&\qquad\text{(cancel)}.\end{aligned}

Need Help ?

Evaluating Difference Quotients

Problem 04\begin{aligned}&\text{Find all the solutions to the following equation: }\\\\& 2x^{3} + 8x^{2} + 6x = 0.\end{aligned} 
Click here to show solution.

Solution:

\begin{aligned}&\text{When you have an expression set equal to zero, it is best to try factoring: } \\\\&\begin{aligned}2x^{3}+8 x^{2}+6 x &= 2 x ( x^{2}+4 x+3 ) &&\qquad\text{(pull out a common factor of } 2x \text{)} \\\\&= 2 x ( x+3 ) ( x+1 ). &&\qquad\text{(factor the quadratic)}\end{aligned} \\\\&\text{Thus we need to solve } \quad 2x(x+3)(x+1)=0. \\\\&\text{Setting each factor equal to zero yields three unique solutions: } \\\\& \quad x=0, \quad x=-3, \quad \text{and} \quad x=-1.\end{aligned}

Need Help ?

Solving Polynomial Equations

Problem 05\begin{aligned}&\text{Find the } x \text { and } y \text { intercepts for the following function: }\\\\& f(x)=x^{3}-9 x\end{aligned} 
Click here to show solution.

Solution:

\begin{aligned}&\text{To find the y-intercept, set } x=0. \\\\&f(0)=0^{3}-9 \cdot 0 = 0. \\\\&\text{Thus, the y-intercept occurs at } y=0. \\\\\\&\text{To find the x-intercept, set } y=0. \\\\&\begin{aligned}0 &= x^{3} - 9x &&\qquad\text{(set y=0)} \\\\&= x ( x^{2}-9 ) &&\qquad\text{(pull out the common factor)} \\\\&= x ( x + 3 ) ( x - 3 ) &&\qquad\text{(difference of squares)}\end{aligned} \\\\&\text{Setting each factor equal to zero yields the three unique x-intercepts:} \\\\&\quad x=0, \quad x=-3, \quad \text{and} \quad x=3.\end{aligned}

Need Help ?

Finding x and y Intercepts

Problem 06\begin{aligned}&\text{Find the equation of the line passing through the point } (5,1) \text{ with slope } 7. \\&\text{Put your final answer in slope-intercept form.}\end{aligned} 
Click here to show solution.

Solution:

\begin{aligned}&\text{First, we can use point-slope form:} \quad y - y_{\circ } = m (x - x_{o} ). \\\\&\text{This gives us the following equation: } \quad y - 1 = 7( x - 5). \\\\&\text{Our goal is to get the equation into slope-intercept form:} \quad y = m x + b. \\\\&\text{So we distribute the 7 and add 1 to both sides.} \\\\&\text{Thus, we get the following equation: } \quad y = 7x - 34.\end{aligned}

Need Help ?

Linear Equations

Problem 07\begin{aligned}\text{Find and simplify } \quad \dfrac{f(2+h)-f(2)}{h} \quad \text{ given } \quad f(x)=\sqrt{x+4}.\end{aligned} 
Click here to show solution.

Solution:

\begin{aligned}\dfrac{f(2+h)-f(2)}{h} &= \dfrac{\sqrt{(2+h)+4} - \sqrt{(2)+4}}{h} &&\qquad\text{(plug into the function)}\\\\&= \dfrac{\sqrt{h+6} - \sqrt{6}}{h} &&\qquad\text{(simplify)} \\\\&= \dfrac{\sqrt{h+6} - \sqrt{6}}{h} \times \dfrac{\sqrt{h+6} + \sqrt{6}}{\sqrt{h+6} + \sqrt{6}} &&\qquad\text {(multiply by the conjugate)} \\\\&= \dfrac{h + 6 - 6}{h (\sqrt{h+6} + \sqrt{6})} &&\qquad\text {(FOIL the numerators)} \\\\&= \dfrac{1}{\sqrt{h+6} + \sqrt{6}} &&\qquad\text {(cancel)}.\end{aligned}

Need Help ?

Evaluating Difference Quotients

Problem 08\begin{aligned}&\text{Graph the following functions: }\\\\&\text{a. } \qquad f(x)=3\cos (2x) \\\\&\text{b. } \qquad g(x)= \ln(x-2)+5\end{aligned} 
Click here to show solution.

Solution:

\begin{aligned}&\text{a. First, recall the graph of } y=\cos x.\\&\text{It passes through the point (0,1) and has period } 2\pi \text{ and amplitude 1.}\\&\text{This function is being stretched vertically by a factor of 3 and squished horizontally by a factor of 2.}\\&\text{Thus, the new amplitude is 3 and the new period is } \pi.\end{aligned}

\begin{aligned}&\text{b. First, recall the graph of the natural log function } y=\ln x.\\&\text{It passes through the point (1,0) and has a vertical asymptote at } x=0.\\&\text{This function is being translated up 5 and to the RIGHT 2.}\\&\text{Thus, the new asymptote is at } x=2 \text{ and the point moves to (3, 5)}.\end{aligned}

Need Help ?

Function Transformations

Problem 09\begin{aligned}&\text{Find all vertical and horizontal asymptotes of the following function:}\\\\&f(x)=\dfrac{(x+3)(x-2)}{(x-4)(x-2)}\end{aligned}
Click here to show solution.

Solution:

\begin{aligned}&\text{Holes occur when there is a factor which appears in both the numerator and the denominator.} \\\\&\text{Since } (x-2) \text{ appears in both the numerator and the denominator, there is a hole at } x=2. \\\\&\text{Vertical asymptotes occur when there is a factor in the denominator which does not appear in the numerator.}\\\\&\text{Since } (x-4) \text{ appears in the denominator, there is a vertical asymptote at } x=4. \\\\&\text{To find horizontal asymptotes, we need to look at the leading terms of the numerator and the denominator.} \\\\&f(x)=\dfrac{(x+3)(x-2)}{(x-4)(x-2)}=\dfrac{x^{2}+x-6}{x^{2}-6x+8}. \\\\&\text{Notice that both the numerator and denominator have a degree of 2 and a leading coefficient of 1.} \\\\&\text{Since the degrees are equal, we take the ratio of the leading coefficients: } y=\dfrac{1}{1}. \\\\&\text{Simplifying this fraction gives us our horizontal asymptote: } y=1.\end{aligned}

Need Help ?

Asymptotes of Rational Functions

Problem 10\text{Simplify the expression: } \quad \dfrac{\quad\dfrac{x}{y}-\dfrac{y}{x}\quad}{\dfrac{1}{y}+\dfrac{1}{x}} 
Click here to show solution.

Solution:

\begin{aligned}\dfrac{\quad\dfrac{x}{y}-\dfrac{y}{x}\quad}{\dfrac{1}{y}+\dfrac{1}{x}} &= \dfrac{\quad\dfrac{x}{x}\dfrac{x}{y}-\dfrac{y}{x}\dfrac{y}{y}\quad}{\dfrac{x}{x}\dfrac{1}{y}+\dfrac{1}{x}\dfrac{y}{y}} &&\qquad\text{(write all fractions with common denominator } xy \text{)} \\\\&= \dfrac{\quad\dfrac{x^{2}}{xy}-\dfrac{y^{2}}{xy}\quad}{\dfrac{x}{xy}+\dfrac{y}{xy}} &&\qquad\text{(all fractions now have same denominator)} \\\\&= \dfrac{\quad\dfrac{x^{2}-y^{2}}{xy}\quad}{\dfrac{x+y}{xy}} &&\qquad\text{(combine fractions with common denominator)} \\\\&= \dfrac{\quad x^{2}-y^{2}\quad}{x+y} &&\qquad\text{(multiply numerator and denominator by } xy \text{)} \\\\&= \dfrac{\quad (x+y)(x-y)\quad}{x+y} &&\qquad\text{(difference of squares)} \\\\&= x-y &&\qquad\text{(cancel } x+y \text{)}. \\\\\end{aligned}

Need Help ?

Complicated Fractions

Problem 11\text{On what intervals is the following function increasing / decreasing ?}
Click here to show solution.

Solution:

\begin{aligned}&\text{A function is increasing when it has a positive slope.}\\&\text{This function is increasing when x is less than -7.}\\&\text{It switches to decreasing when x is between -7 and 0.}\\&\text{Then, it increases from 0 to 7 and decreases after 7.}\\&\text{Using interval notation, we would write: }\\\\&\text{Increasing when x is in the set: } \qquad (-\infty, -7) \cup (0, 7) \\\\&\text{Decreasing when x is in the set: } \qquad (-7, 0) \cup (7, \infty)\\\\&\text{Notice that each set is made of two non-overlapping disjoint intervals.}\\&\text{We use the union symbol } (\cup) \text{ to create a set which contains all the points from both intervals.}\end{aligned}

Need Help ?

Increasing & Decreasing Intervals

Problem 12\text{Simplify the following expression: } \qquad \dfrac{x^{2} \cos (x)-3 x^{3} \sin (x)}{x^{2}} 
Click here to show solution.

Solution:

\begin{aligned}\frac{x^{2} \cos (x)-3 x^{3} \sin (x)}{x^{2}} &= \frac{x^{2}(\cos (x)-3 x \sin (x))}{x^{2}} &&\qquad\text{(pull out common factor)} \\\\&= \cos (x)-3 x \sin (x) &&\qquad\text{(cancel)}.\end{aligned}

Need Help ?

Simplifying Trig Expressions

Problem 13\text{Simplify the following expression: } \qquad \dfrac{\cos (\theta)}{7 \sin (\theta) \csc (\theta)} 
Click here to show solution.

Solution:

\begin{aligned}\dfrac{\cos(\theta)}{7\sin(\theta)\csc(\theta)}&= \dfrac{\cos(\theta)}{7\sin(\theta)\left(\dfrac{1}{\sin(\theta)}\right)} && \qquad \text{(definition of cosecant)} \\\\&= \dfrac{\qquad\cos(\theta)\qquad}{\dfrac{7\sin(\theta)}{\sin(\theta)}} && \qquad \text{(write denominator as one fraction)} \\\\&= \dfrac{\cos(\theta)}{7} && \qquad \text{(cancel)} \\\\&= \dfrac{1}{7}\cos \theta && \qquad \text{(simplify)}. \\\\\end{aligned}

Need Help ?

Simplifying Trig Expressions

Problem 14\begin{aligned}&\text{Find } f(x) \text{ and } g(x) \text{ such that } h(x)=f(g(x)). \\\\&\text{a.}\qquad h(x)=\sqrt{2 x^{2}-3 x} \\\\&\text{b.}\qquad h(x)=e^{\tan x}\end{aligned} 
Click here to show solution.

Solution:

\begin{aligned}&\text{a.} &&\quad f(x)=\sqrt{x} \qquad\text{and}\qquad g(x)=2x^{2}-3x. \\\\& &&\quad \text{Checking the solution: }\quad f(g(x)) = \sqrt{g(x)} = \sqrt{2 x^{2}-3 x} = h(x). \\\\&\text{b.} &&\quad f(x)=e^{x} \qquad\text{and}\qquad g(x)=\tan x. \\\\& &&\quad \text{Checking the solution: }\quad f(g(x)) = e^{g(x)} = e^{\tan x} = h(x). \\\\\end{aligned}

Need Help ?

Composition of Functions

Problem 15\text{Write an equation which relates the following quantities: }
 

Click here to show solution.

Solution:

\begin{aligned}&\text{Notice that the side of length x is located OPPOSITE from the angle theta.}\\&\text{The side of length 5 is located ADJACENT to the angle theta.}\\&\text{The tangent function relates these quantities: \quad tan( ANGLE ) = OPPOSITE / ADJACENT}.\\\\&\text{Thus, } \tan \theta = \dfrac{x}{5}.\end{aligned}

Need Help ?

Triangle Trig Ratios

Math Course Prep Feedback Form

Please take a few moments to fill out the anonymous feedback form below: