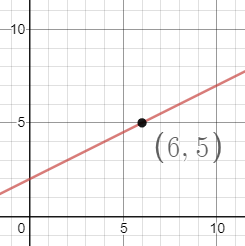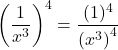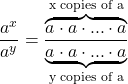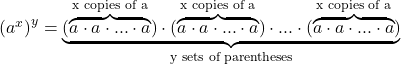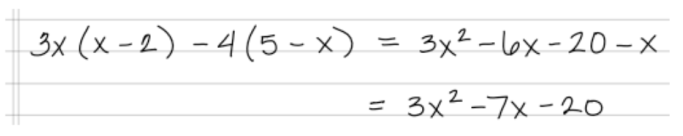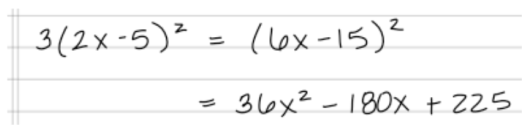MAT 122 Course Prep
Note: This page contains LaTeX markup to display mathematical notation.
This collection of problems is meant to provide practice for a range of skills needed for MAT 122. Read and attempt each problem first; if you aren’t sure how to start a problem, explore the resources on the right to refresh your memory and try again. A drop-down button is found beneath each problem for you to compare both your logic and final answers. Keep track of the skills you aren’t comfortable with, and reacquaint yourself with them so you’re fully prepared for the topics you’ll grapple with soon. Get help in the Math Lab. Return to the Course Prep page.
Problem 1: Evaluate the following expressions. Remember to follow the order of operations.
| Part a. | Click here to show solution.Everything before the division sign is part of the numerator, and everything after it is part of the denominator. In the numerator, the 4 is located inside 3 sets of parentheses, so we must start there. It is being multiplied by 5, so we replace 5(4) with 20. In the denominator, the -2 is inside two sets of parentheses, and it is being multiplied by 5, so we replace 5(-2) with -10.
Again looking at the numerator, inside the inner parentheses, we can evaluate 9 – 20 + 3 = -8. In the denominator, we can evaluate -10 – 1 = -11.
The numerator can be simplified by evaluating -5 + (-8) = -13. Since both the numerator and denominator are negative, the result will be positive. Thus, our final answer is:
| Need Help ? |
Problem 2: Find the value of y using the given value of x.
| Part a. | Click here to show solution.Since x = 4, we can replace every x in the first equation with a 4:
Order of operations tells us that we need to square the 4 and then multiply by -1, and also multiply 2 and 4:
Thus, our final answer is: | Need Help ? |
| Part b. | Click here to show solution.Since x = -3, we can replace every x in the first equation with a -3:
Order of operations tells us that we need to square the -3 first, which means -3 times -3. This makes 9 because the negatives cancel. Also, we need to multiply 2 and -3, which makes -6:
Now we can make the 9 negative, but the 6 ends up positive because the two minus signs cancel:
Thus, our final answer is: | |
| Part c. | Click here to show solution.Since x = -2, we can replace every x in the first equation with a -2:
Order of operations tells us that we need evaluate the insides of every set of parentheses first, so:
Now we can multiply these three numbers in any order, so let’s do 5 times 1 is 5, and then multiplying by -10 gives us -50. Thus, our final answer is: | |
| Part d. | Click here to show solution.Since x = -3, we can replace every x in the first equation with a -3:
Now we must simplify the expressions inside every set of parentheses:
This means 4 times 0 times -11. Remember that any number times zero is equal to zero.
|
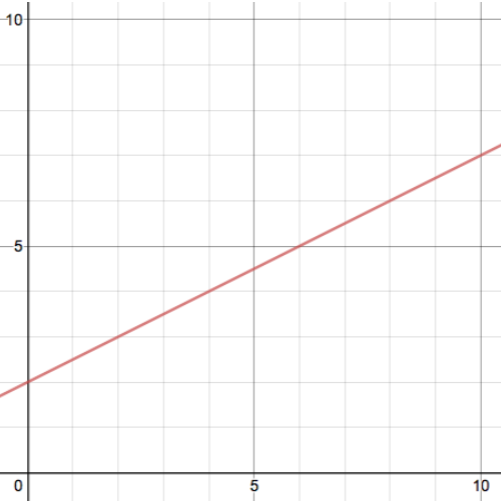
Problem 3: Use the following graph to answer the questions below.
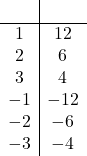
Problem 4: Complete the following table.
| Part a. | 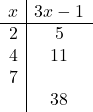 Click here to show solution.First, we will try to fill in the blank space next to the 7.
Simplifying, we find that when x = 7:
Next, we can try to fill the blank space in the first column next to 38. Adding 1 to both sides gives us:
Our next step will be to divide both sides by 3. Thus, we have found that when 3x – 1 = 38:
Our completed table looks like this:
| Need Help ? |
Problem 5: Solve the following equations.
| Part a. | Click here to show solution.First, we can replace the decimal 0.2 with its fraction equivalent and simplify:
Now we can see that, to isolate x, we need to multiply both sides by 5:
| Need Help ? |
| Part b. | Click here to show solution.Our goal is to isolate x. First, we can subtract 8 from both sides, and on the left side, we will get 44 – 8 = 36:
Our last step is to divide both sides by -6, which is going to leave x alone on the right side, and will make:
Finally, we can recall that 36 is 6 times 6, and we can pull the negative sign out front, because a positive divided by a negative results in a negative answer. Thus, we get:
| |
| Part c. | Click here to show solution.Notice that x appears on both sides, so we need to combine those like terms. We can add 3x to both sides, which will give us 5x on the left and no x on the right:
Now we can get rid of the 14 by subtracting from both sides, and calculating 9 – 14 = -5:
Our last step is to divide by 5 on both sides:
| |
| Part d. | Click here to show solution.We could deal with the 3 in the denominator first (multiply both sides by 3) and then deal with the 4 in the numerator (divide both sides by 4), but there is another way. Since the fraction 4/3 is the coefficient of x, we can simply divide both sides by 4/3:
Recall that dividing by a fraction is the same as multiplying by the reciprocal:
We can write -80 as a fraction, and multiply the numerators and denominators separately:
We can simplify this to get:
|
Problem 6: Answer the following questions.
| Captain Tim’s boat caught 360 lobsters.
Captain Steve’s boat caught 450 lobsters. | Need Help ? | |
| Part a. | The number of lobsters caught by Captain Tim’s boat is what percent of the number of lobsters caught by Captain Steve’s boat ?Click here to show solution.First, we will determine the ratio:
Simplifying this fraction, we can divide the numerator and denominator by 10:
And then we can divide the numerator and denominator by 9:
Now, to get a percent, we want the denominator to equal 100. So we can multiply the numerator and denominator by 20:
A percent is just the numerator of a fraction with a denominator of 100. Thus, our final answer is: | |
| Part b. | The number of lobsters caught by Captain Steve’s boat is what percent of the number of lobsters caught by Captain Tim’s boat ?Click here to show solution.First, we will determine the ratio:
Notice that this fraction is simply the reciprocal of the fraction we found in part a. The fraction from part a simplified to 4/5, so this one must simplify to 5/4.
Now, to get a percent, we want the denominator to equal 100. So we can multiply the numerator and denominator by 25:
A percent is just the numerator of a fraction with a denominator of 100. Thus, our final answer is: |
Problem 7: Rewrite each expression in the form: xa (this is called base-exponent form).
| Part a. | Click here to show solution.We can move a factor from the denominator to the numerator as long as we change the sign of the exponent:
If it seems like the 1 in the numerator disappeared, remember that multiplying by one won’t change the value of
If we want to show all the steps, we could write:
| Need Help ? |
| Part b. | Click here to show solution.We can rewrite radical expressions using fractional exponents. For a square root, we use the fraction 1/2:
If this seems strange, think of it this way: 20 = 1 and 21 = 2 so we would expect that | |
| Part c. | Click here to show solution.We can distribute an exponent over division, which means the 4 becomes the exponent of the 1 in the numerator and the x^3 in the denominator:
Now 1 multiplied by itself 4 times is still 1, but in the denominator we have to combine the exponents. Recall that successive exponents can be combined by multiplication:
Finally, we can rewrite this by moving the x into the numerator, and changing its exponent from positive to negative:
We could also have written out 4 copies of the original fraction:
This could then be expanded as:
| |
| Part d. | Click here to show solution.Recall that the 3 is called the index of the root, and indicates that this is not a square root but a cube root. Following our earlier rule, we can rewrite this root using a 1/3 exponent:
Exponent rules allow us to multiply successive exponents, so we calculate 2 times 1/3 to get 2/3 as the exponent:
|
Problem 8: Solve the following problems by setting up a proportion and solving.
| Part a. | If 6 dogs require 42 kilograms of kibble for a week’s stay at a kennel, how much kibble is required for a week’s stay for 8 dogs ?Click here to show solution.Since the ratio between amount of food and number of dogs is assumed to be constant, we can set up a proportion, which means setting two fractions equal to each other. We know that 42 kg of food divided among 6 dogs must be equal to some unknown amount of food divided among 8 dogs:
Now we can simplify the left side, where 42 divided by 6 equals 7:
At 7 kilograms per dog, it would take 8 times 7 equals 56 kilograms to feed 8 dogs. Thus, to feed 8 dogs for a week, it would take | Need Help ? |
Problem 9: Solve the following problem.
| Part a. | You ate 3/4 of a frozen lasagna. If the label on the package states that 1/3 of a lasagna is a serving, how many servings of lasagna did you eat ?Click here to show solution 1.If 1/3 of a lasagna is equal to 1 serving, then there are 3 servings in a whole lasagna. We want to know how many servings there are in 3/4 of a lasagna. This is like asking how many times 1/3 goes into 3/4. It may help to write 1/3 and 3/4 with a common denominator, so rewrite 1/3 as 4/12 and rewrite 3/4 as 9/12. Now we can see that 1/3 goes into 3/4 two whole times, and there is a remainder of 1/12. 1/12 is actually 1/4 of a serving, so our answer is that you ate 2 and 1/4 servings. Instead, we could write this division problem as a fraction of fractions, and then simplify it. With fractions, we can multiply the numerator and denominator by the same thing without changing the value of the overall fraction. In this case, we multiply the top and bottom by 3:
Thus, our answer is that you ate Notice that 9/4 is equal to 2 and 1/4.
Click here to show solution 2.If 1/3 of a lasagna is equal to 1 serving, then a whole lasagna must be equal to 3 servings. You ate 3/4 of a whole lasagna, so you ate 3/4 of 3 servings. Often in math, the word “of” means multiplication. Thus, we can calculate that you ate:
Writing the 3 as a fraction, we can multiply across to get:
Recall that the fraction 9/4 can be thought of as 4/4 + 4/4 + 1/4 which means 2 and 1/4. As a decimal, we could write this as: 2.25 You ate more than 2 servings. You probably ate more than you should’ve.
| Need Help ? |
Problem 10: Explain in words why the following properties of exponents make sense.
| Recall the meaning of an exponent: ax means x copies of a multiplied together.
Use this to explain in words why the following properties of exponents make sense. | Need Help ? | |
| Part a. | Click here to show solution.If you are multiplying x copies of a and y copies of a all together, then in total you will be multiplying x+y copies of a.
| |
| Part b. | Click here to show solution.Division is the inverse of multiplication, so if you are multiplying x copies of a, and then dividing by y copies of a, then some of those copies will cancel out, and you will have x-y copies left over.
| |
| Part c. | Click here to show solution.If you are multiplying x copies of a, and then you take the result and multiply y copies of that, then you are really multiplying xy copies of a.
|
Problem 11: Verify that each statement is false and then correct it.
Problem 12: Expand the following expressions. Remember to use FOIL.
| F.O.I.L. stands for First, Outer, Inner, Last. When two binomials are being multiplied together, we can use FOIL to remember all the products that appear in the expansion. For example:
| Need Help ? | |
| Part a. | Click here to show solution.Following FOIL will give us the following:
We can take each product and simplify it as:
Now we can combine 6x and 4x to make 10x:
| |
| Part b. | Click here to show solution.Following FOIL will give us the following:
We can take each product and simplify it as:
Now we can combine -3x and 8x to make 5x:
| |
| Part c. | Click here to show solution.Following FOIL will give us the following:
We can take each product and simplify it as:
Notice how -x times -7 gave us a positive result, because the negatives cancel each other. Now we can combine 7x and 2x to make 9x:
| |
| Part d. | Click here to show solution.Following FOIL will give us the following:
We can take each product and simplify it as:
Notice how the first term is positive, because it is the product of two negatives. This is also true of the third term, 1x. Also, instead of writing 1x, we usually just write x, and the coefficient of 1 is implied Now we can combine -5x and x to make -4x:
|
Problem 13: Rewrite each expression in factored form.
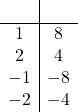
| Part a. | Click here to show solution.List the factors of the constant term, 12:
Notice that we include pairs where both numbers are negative. We want to choose the pair that adds up to the coefficient of x, which is 8, so we pick 2 and 6.
| Need Help ? |
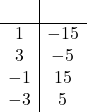
| Part b. | Click here to show solution.List the factors of the constant term, 8:
Notice that we include pairs where both numbers are negative. We want to choose the pair that adds up to the coefficient of x, which is 9, so we pick 1 and 8.
| |
| Part c. | Click here to show solution.List the factors of the constant term, -15:
Notice that we include each pair twice, once with the smaller number negative and once with the larger number negative. We want to choose the pair that adds up to the coefficient of x, which is 2, so we pick -3 and 5, because adding them together gives us -3 + 5 = 2.
| |
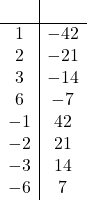
| Part d. | Click here to show solution.List the factors of the constant term, -42:
Notice that we include each pair twice, once with the smaller number negative and once with the larger number negative. We want to choose the pair that adds up to the coefficient of x, which is -1, so we pick 6 and -7, because when we add them together we get 6 + -7 = -1.
| |
| Part e. | Click here to show solution.List the factors of the constant term, 12:
Notice that we include pairs where both numbers are negative. We want to choose the pair that adds up to the coefficient of x, which is -7, so we need to pick two negative numbers. We pick -3 and -4 because adding them gives us -3 + -4 = -7
| |
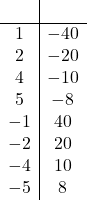
| Part f. | Click here to show solution.List the factors of the constant term, -40:
Notice that we include each pair twice, once with the smaller number negative and once with the larger number negative. We want to choose the pair that adds up to the coefficient of x, which is 3, so we pick -5 and 8, because when we add them together we get -5 + 8 = 3.
|
Problem 14: Use the area diagram to answer the questions.
Math Course Prep Feedback Form
Please take a few moments to fill out the anonymous feedback form below: