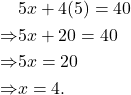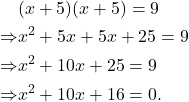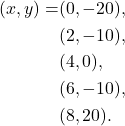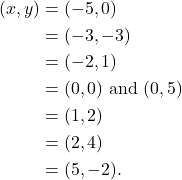MAT 116 Course Prep
Note: This page contains LaTeX markup to display mathematical notation.
This collection of problems is meant to provide practice for a range of skills needed for MAT 116. Read and attempt each problem first; if you aren’t sure how to start a problem, explore the resources on the right to refresh your memory and try again. A drop-down button is found beneath each problem for you to compare both your logic and final answers. Keep track of the skills you aren’t comfortable with, and reacquaint yourself with them so you’re fully prepared for the topics you’ll grapple with soon. Get help in the Math Lab. Return to the Course Prep page.
Problem 1: Identify whether the given statement is an expression or an equation. If it is an equation, determine if it is also an identity. Determine whether each term in the statement is constant or variable.
| Part a | Click here to show solution.Solution: This first statement is an equation since there is an equal sign, but it is not an identity since we can choose a value of | Video: Variables, Expressions, and Equations |
| Part b | Click here to show solution.Solution: | |
| Part c | Click here to show solution.Solution: | |
| Part d | Click here to show solution.Solution: | |
| Part e | Click here to show solution.Solution: | |
| Part f | Click here to show solution.Solution: | |
| Part g | Click here to show solution.Solution: | |
| Part h | Click here to show solution.Solution: |
Problem 2: Rewrite the following expressions in the form ![]() , where
, where ![]() and
and ![]() are real numbers.
are real numbers.
| Part a | Click here to show solution.Solution: | Video: Intro to Rational Exponents |
| Part b | Click here to show solution.Solution: | Video: Rewriting Roots as Rational Exponents |
| Part c | Click here to show solution.Solution: | |
| Part d | Click here to show solution.Solution: | Video: Exponents in denominators |
| Part e | Click here to show solution.Solution: | |
| Part f | Click here to show solution.Solution: | |
| Part g | Click here to show solution.Solution: | Video: Intro to Rational Expression Simplification |
| Part h | Click here to show solution.Solution: |
Problem 3: Given that ![]() ,
, ![]() ,
, ![]() , simplify the following expressions. If possible, find exact values.
, simplify the following expressions. If possible, find exact values.
| Part a | Click here to show solution.Solution: | Video: Worked Example: Evaluating Functions from Equation |
| Part b | Click here to show solution.Solution: | |
| Part c | Click here to show solution.Solution: | |
| Part d | Click here to show solution.Solution: | |
| Part e | Click here to show solution.Solution: | |
| Part f | Click here to show solution.Solution: | |
| Part g | Click here to show solution.Solution: | |
| Part h | Click here to show solution.Solution: |
Problem 4: Solve the following equations for x, and verify your solution.
| Part a | Click here to show solution.Solution: To give you an idea of what it would look like if we somehow got the incorrect answer, pretend we solved the original equation and got | Video: Solving Linear Equations IWrite-up: One Step Equations |
| Part b | Click here to show solution.Solution: | |
| Part c | Click here to show solution.Solution: | Video: Solving Linear Equations IIWrite-up: Two Step Equations |
| Part d | Click here to show solution.Solution: | |
| Part e | Click here to show solution.Solution: | Video: Solving Equations with Rational Exponents |
| Part f | Click here to show solution.Solution: | |
| Part g | Click here to show solution.Solution: | |
| Part h | Click here to show solution.Solution: |
Problem 5: Given ![]() , either find the value of the given expression or solve the given equation for x.
, either find the value of the given expression or solve the given equation for x.
| Part a | Click here to show solution.Solution: | |
| Part b | Click here to show solution.Solution: | Write-up: Simplifying Fractions |
| Part c | Click here to show solution.Solution: | |
| Part d | Click here to show solution.Solution: | Video: Worked Example: Using the Quadratic FormulaWrite-up: The Quadratic Formula |
Problem 6: Expand the following expressions.
| Part a | Click here to show solution.Solution: | Video: Multiplying BinomialsWrite-up: FOIL Method |
| Part b | Click here to show solution.Solution: |
Problem 7: Find the slope of the line passing through the following points.
| Part a | (0,5) and (4,19)Click here to show solution.Solution: | Worked Example: Slope from Two PointsWrite-up: Slope Formula |
| Part b | (2,11) and (3,-3)Click here to show solution.Solution: | |
| Part c | Click here to show solution.Solution: |
Problem 8: Find the equation of the line passing through the following points.
| Part a | (0,5) and (4,19)Click here to show solution.Solution: In slope-intercept form, the slope and y-intercept of the line need to be known (unsurprisingly). We calculated the slope between these points above: In point-slope form, the slope and any one point on the line must be known (unsurprisingly). Choose Point-slope form is generally more helpful, as needing any point on the line is a less strict requirement than knowing the y-intercept. The slope is needed in either case. | Video: Point-Slope and Slope-Intercept EquationsWrite-up: Slope-Intercept Form |
| Part b | (2,11) and (3,-3)Click here to show solution.Solution: | |
| Part c | Click here to show solution.Solution: |
Problem 9: From the table below, identify the points and write them in the form (x,y).
| Part a |
Click here to show solution.Solution: |
Problem 10: Identify the points on the following x-y plane and write them in the form (x,y).
| Part a | 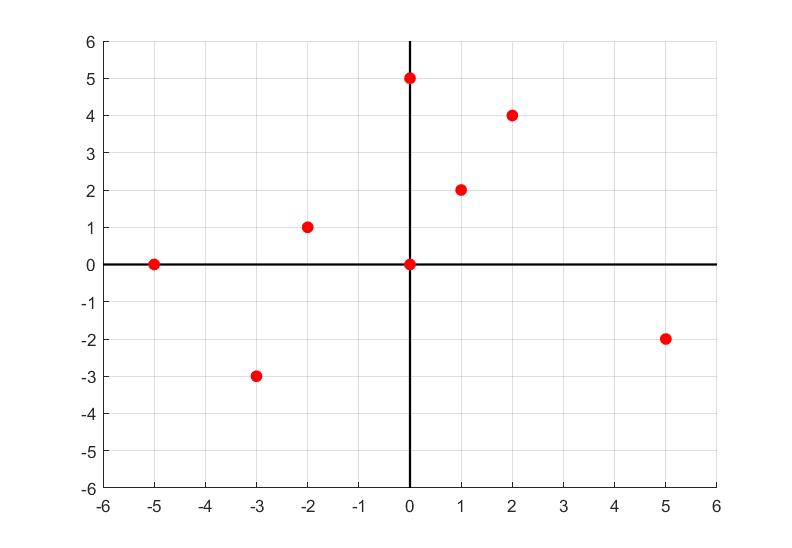 Click here to show solution.Solution: | Video: Introduction to the Coordinate Plane |
Problem 11: Find the area of the following figures (including units).
| Part a | A rectangle with a length of 5 meters and width of 9 meters.Click here to show solution.Solution: | |
| Part b | A square with side length 7 inches.Click here to show solution.Solution: | |
| Part c | A triangle whose base is 20 cm and whose height is 11 cm.Click here to show solution.Solution: | |
| Part d | A circle of radius 4 feet.Click here to show solution.Solution: |
Math Course Prep Feedback Form
Please take a few moments to fill out the anonymous feedback form below: