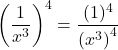MAT 115 Course Prep
Note: This page contains LaTeX markup to display mathematical notation.
This collection of problems is meant to provide practice for a range of skills needed for MAT 115. Read and attempt each problem first; if you aren’t sure how to start a problem, explore the resources on the right to refresh your memory and try again. A drop-down button is found beneath each problem for you to compare both your logic and final answers. Keep track of the skills you aren’t comfortable with, and reacquaint yourself with them so you’re fully prepared for the topics you’ll grapple with soon. Get help in the Math Lab. Return to the Course Prep page.
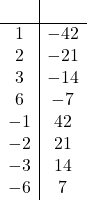
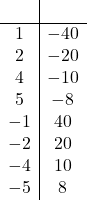
Problem 1: Using the functions defined below, simplify each expression. If possible, find exact values.
| Part a. | Click here to show solution.
| Video: Worked Example: Evaluating Functions from Equation |
| Part b. | Click here to show solution.
| |
| Part c. | Click here to show solution.
| |
| Part d. | Click here to show solution.
| |
| Part e. | Click here to show solution.
| |
| Part f. | Click here to show solution.
| |
| Part g. | Click here to show solution.
| |
| Part h. | Click here to show solution.
|
Problem 2: Solve the following equations for x, and verify your solution.
| Part a. | Click here to show solution.Divide both sides by 0.2: To give you an idea of what it would look like if we somehow got the incorrect answer, pretend we solved the original equation and got | Video: Solving Linear Equations IWrite-up: One Step Equations |
| Part b. | Click here to show solution.Divide both sides by | |
| Part c. | Click here to show solution.Begin by subtracting 8 from each side, yielding | Video: Solving Linear Equations IIWrite-up: Two Step Equations |
| Part d. | Click here to show solution.On the left-hand side, a factor of | |
| Part e. | Click here to show solution.To isolate the | Video: Solving Equations with Rational Exponents |
| Part f. | Click here to show solution.In a similar fashion as the previous problem, raise both sides to the | |
| Part g. | Click here to show solution.In earlier questions, | |
| Part h. | Click here to show solution.In a similar fashion as the previous problem, we simply aim to isolate |
Problem 3: Expand the following expressions.
| Part a. | Click here to show solution.This can be rewritten as | Video: Multiplying BinomialsWrite-up: FOIL Method |
| Part b. | Click here to show solution.Following the same logic as the last problem, the multiplication gives |
Problem 4: Find the slope of the line passing through the following points.
| Part a. | (0,5) and (4,19)Click here to show solution.Slope (commonly denoted by the symbol | Worked Example: Slope from Two PointsWrite-up: Slope Formula |
| Part b. | (2,11) and (3,-3)Click here to show solution.Following the same logic as the previous problem, we have | |
| Part c. | Click here to show solution.This represents the general case: |
Problem 5: Find the equation of the line passing through the following points.
| Part a. | (0,5) and (4,19)Click here to show solution.There are two lanes of thought here, corresponding to the two different generic forms of a line: slope-intercept form In slope-intercept form, the slope and y-intercept of the line need to be known (unsurprisingly). We calculated the slope between these points above: In point-slope form, the slope and any one point on the line must be known (unsurprisingly). Choose Point-slope form is generally more helpful, as needing any point on the line is a less strict requirement than knowing the y-intercept. The slope is needed in either case. | Video: Point-Slope and Slope-Intercept EquationsWrite-up: Slope-Intercept Form |
| Part b. | (2,11) and (3,-3)Click here to show solution.We don’t know the y-intercept here, so use point-slope form with either of the points provided. For the purpose of this example, we’ll use | |
| Part c. | Click here to show solution.Use point-slope form again. For slope, recall that |
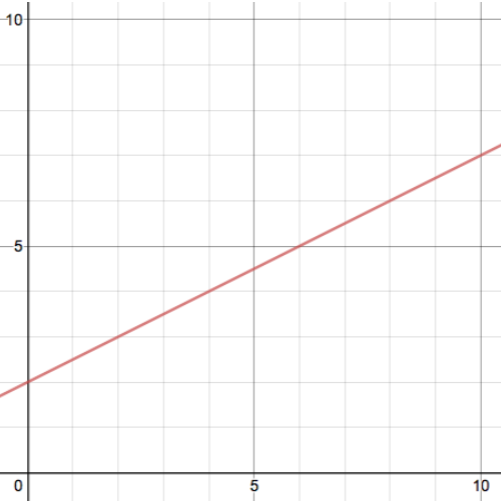
Problem 6: Use the following graph to answer the questions below.
 | Need Help ?MathPlanet – Coordinates & Ordered Pairs | |
| Part a. | Does the point (6, 5) fall on the graph of the line ?Click here to show solution.A coordinate point tells you the x-coordinate first, followed by the y-coordinate. We can see that the point (6, 5) has an x-coordinate of 6. We can see on the x-axis, between 0 and 5, that this region is divided into 5 equal parts, marked by the light grey lines. This means that each square cell on the grid is one unit wide. To find 6 on the x-axis, we just need to go one unit to the right of the 5. Then, we follow the light grey vertical grid-line up to the red line, and we have found the point on the line with x-coordinate 6. Finally, we follow the light grey horizontal grid-line from this point to the left, until we reach the y-axis. This horizontal grid-line intersects the y-axis right at the number 5, so we know that 5 is the y-coordinate that corresponds to the x-coordinate of 6. 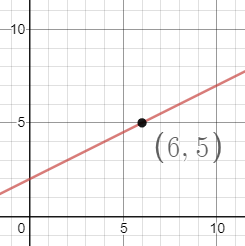 Thus, we have determined that (6, 5) does in fact fall on the graph of the line. |
Problem 7: Rewrite each expression in the form: xa (this is called base-exponent form).
| Part a. | Click here to show solution.We can move a factor from the denominator to the numerator as long as we change the sign of the exponent:
If it seems like the 1 in the numerator disappeared, remember that multiplying by one won’t change the value of
If we want to show all the steps, we could write:
| Need Help ?BrownMath – Negative and Fractional Exponents |
| Part b. | Click here to show solution.We can rewrite radical expressions using fractional exponents. For a square root, we use the fraction 1/2:
If this seems strange, think of it this way: 20 = 1 and 21 = 2 so we would expect that | |
| Part c. | Click here to show solution.We can distribute an exponent over division, which means the 4 becomes the exponent of the 1 in the numerator and the x^3 in the denominator:
Now 1 multiplied by itself 4 times is still 1, but in the denominator we have to combine the exponents. Recall that successive exponents can be combined by multiplication:
Finally, we can rewrite this by moving the x into the numerator, and changing its exponent from positive to negative:
We could also have written out 4 copies of the original fraction:
This could then be expanded as:
| |
| Part d. | Click here to show solution.Recall that the 3 is called the index of the root, and indicates that this is not a square root but a cube root. Following our earlier rule, we can rewrite this root using a 1/3 exponent:
Exponent rules allow us to multiply successive exponents, so we calculate 2 times 1/3 to get 2/3 as the exponent:
|
Problem 8: Expand the following expressions. Remember to use FOIL.
| F.O.I.L. stands for First, Outer, Inner, Last.When two binomials are being multiplied together, we can use FOIL to remember all the products that appear in the expansion. For example:
| Need Help ?MathPlanet – Multiplication of Polynomials | |
| Part a. | Click here to show solution.Following FOIL will give us the following:
We can take each product and simplify it as:
Now we can combine 6x and 4x to make 10x:
| |
| Part b. | Click here to show solution.Following FOIL will give us the following:
We can take each product and simplify it as:
Now we can combine -3x and 8x to make 5x:
| |
| Part c. | Click here to show solution.Following FOIL will give us the following:
We can take each product and simplify it as:
Notice how -x times -7 gave us a positive result, because the negatives cancel each other. Now we can combine 7x and 2x to make 9x:
| |
| Part d. | Click here to show solution.Following FOIL will give us the following:
We can take each product and simplify it as:
Notice how the first term is positive, because it is the product of two negatives. This is also true of the third term, 1x. Also, instead of writing 1x, we usually just write x, and the coefficient of 1 is implied Now we can combine -5x and x to make -4x:
|
Problem 9: Rewrite each expression in factored form.
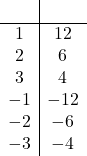
| Part a. | Click here to show solution.List the factors of the constant term, 12:
Notice that we include pairs where both numbers are negative. We want to choose the pair that adds up to the coefficient of x, which is 8, so we pick 2 and 6.
| Need Help ?MathPlanet – Factoring Quadratics |
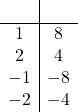
| Part b. | Click here to show solution.List the factors of the constant term, 8:
Notice that we include pairs where both numbers are negative. We want to choose the pair that adds up to the coefficient of x, which is 9, so we pick 1 and 8.
| |
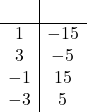
| Part c. | Click here to show solution.List the factors of the constant term, -15:
Notice that we include each pair twice, once with the smaller number negative and once with the larger number negative. We want to choose the pair that adds up to the coefficient of x, which is 2, so we pick -3 and 5, because adding them together gives us -3 + 5 = 2.
| |
| Part d. | Click here to show solution.List the factors of the constant term, -42:
Notice that we include each pair twice, once with the smaller number negative and once with the larger number negative. We want to choose the pair that adds up to the coefficient of x, which is -1, so we pick 6 and -7, because when we add them together we get 6 + -7 = -1.
| |
| Part e. | Click here to show solution.List the factors of the constant term, 12:
Notice that we include pairs where both numbers are negative. We want to choose the pair that adds up to the coefficient of x, which is -7, so we need to pick two negative numbers. We pick -3 and -4 because adding them gives us -3 + -4 = -7
| |
| Part f. | Click here to show solution.List the factors of the constant term, -40:
Notice that we include each pair twice, once with the smaller number negative and once with the larger number negative. We want to choose the pair that adds up to the coefficient of x, which is 3, so we pick -5 and 8, because when we add them together we get -5 + 8 = 3.
|
Problem 10: Solve the linear inequality.
| Part a. | Click here to show solution.Notice that there are terms containing x on both sides of the inequality. First, we can subtract 4x from both sides so that we can combine these like terms:
Now we can move all the constants to the other side, which means we must add 13 to both sides:
Finally, we can divide both sides by 3 to isolate the variable:
This says 6 is less than x, which is another way of saying that x is greater than 6. Thus, we have: | Need Help ?Video: KhanAcademy – Solving Inequalities |
Problem 11: Express the following using interval notation.
| Part a. | Click here to show solution.The statement literally says that 7 is less than x, which is less than 13. In other words, x is greater than 7 and x is less than 13. This indicates a single interval, from 7 to 13. Because the original statement uses We use “soft brackets” (parentheses) to indicate that the interval includes all numbers between 7 and 13, but does NOT include the endpoints:
| Need Help ?Video: KhanAcademy – Interval Notation |
| Part b. | Click here to show solution.The statement literally says that -16 is less than or equal to x, which is less than or equal to 10. In other words, x not greater than 10, and is not less than -16. This indicates a single interval with endpoints at -16 and 10. Because the original statement uses We use “hard brackets” [square braces] to indicate that the interval includes all numbers between 7 and 13 and ALSO includes the endpoints:
| |
| Part c. | Click here to show solution.Compared to the previous two problems, we simply need to use a hard bracket to start our interval, because the -8 is NOT included, and a soft bracket to end the interval, because the -4 IS included.
| |
| Part d. | Click here to show solution.The statement says x is greater than 56. This excludes the possibility that x = 56, so we will use a soft bracket. All the numbers greater than 56 together form a sort of interval with a left endpoint at 56, but no right endpoint. Since the interval starts at 56 and never ends, we can think of the right endpoint as being “at” infinity. Infinity is not a number, so we do not want to include it, which means we must use a soft bracket here as well. Using infinity as our right endpoint means that all numbers between 56 and infinity are included, even if both endpoints are not.
| |
| Part e. | Click here to show solution.The statement says that x is less than or equal to -42. This includes the possibility that x = -42, so we must use a hard bracket. Since all negative numbers less than -42 are included in this interval, we need to start our interval at negative infinity (but not include it). -42 is actually where our interval ends. In other words, negative infinity is the left endpoint of this interval, and -42 is the right endpoint.
|
Problem 12: Solve using the quadratic formula to get exact answers (expressed using radicals).
| Part a. | Click here to show solution.Recall the quadratic formula:
In the quadratic equation given above, we can see that a = 1, b = -8, and c = 5. Notice that, even thought there is no visible coefficient in front of the x2 term, we always assume a coefficient of 1, which is why a = 1. Also, the minus sign in front of the 8 must be included in the b value, which is why we have b = -8.
Notice how we placed parentheses around every place where we plugged in a value. Now we want to simplify -(-8) = 8 and (-8)2 = 64 and 4(1)(5) = 20 and 2(1) = 2.
Since 64 – 20 = 44, and 44 = 4 times 11, we can write:
4 is a square number, so we can pull it out from under the square root as a 2:
Now, we can divide by 2. Recall that each term in the numerator must be divided by 2:
Finally, recall that the symbol
| Need Help ?Video: KhanAcademy – Quadratic Formula |
Math Course Prep Feedback Form
Please take a few moments to fill out the anonymous feedback form below: