Abstracts
Friday, August 10, 2012. Master’s Thesis Defense.
Heidi Qiu, UMaine Master’s candidate in Statistics (Advisor: Ramesh Gupta).
“Analysis of survival data by an exponential-generalized Poisson distribution”
11:00 am, 421 Neville Hall.
Survival models incorporating a cure fraction, often referred to as “cure rate models” are becoming increasingly popular in analyzing data from cancer clinical trials. In this model, we assume that a fraction of the population is cured and the remaining population is uncured after the first treatment. In this thesis, we consider the uncured population where the number (N) of metastasis-competent cells (clonogens) is unknown and the event occurs as soon as one of the clonogens metastasizes. An exponential-generalized Poisson distribution (EGP) is developed, where the distribution of N is taken as generalized Poisson. This is a generalization of the Poisson distribution having one extra parameter. The structural properties of the resulting distribution are presented and the maximum likelihood estimation of the parameters is investigated. Extensive simulation studies are carried out to study the performance of the estimations. A score test is developed to test the importance of the extra parameter. Two real data sets are examined and it is shown that the EGP model presented here fits better than the exponential Poisson distribution.
Tuesday, April 24, 2012. Graduate Seminar.
Heidi Qiu, UMaine Master’s student in Statistics.
“A New Lifetime Distribution”
3:10 pm – 4:00 pm, 421 Neville Hall.
A population whose behavior over time is characterized by ‘work-hardening’ or ‘immunity’ is expected to exhibit decreasing failure rate. The distributions with decreasing failure rate are of great interests in recent years. After introducing a new lifetime distribution which is obtained by compounding exponential and zero truncated Poisson distribution,there will be a brief introduction to EM algorithm, a general method for estimating parameters in application to missing data and mixture density problems. EM algorithm will be used to determine the maximum likelihood estimates of the introduced lifetime distribution and an illustrative example will be presented.
Monday, April 23, 2012. Graduate Seminar.
Joshua Case, UMaine Master’s student in Mathematics.
“An Introduction to Gray Permutations”
2:10 pm – 3:00 pm, 421 Neville Hall.
The Binary Reflected Gray Code (BRGC) is an algorithm which allows us to list all binary strings of length n so that successive strings differ by one bit. A Gray permutation generalizes this scheme and refers to any method of listing elements from a set S so that adjacent objects obey some simple rule. We can associate this rule with a graph G where the vertices of G are the elements of S. Two elements are joined by an edge if they satisfy our rule. Therefore, a Hamiltonian cycle or path in G is a Gray permutation. We will discuss the BRGC as a Gray permutation and examine a Gray permutation that naturally arises in the scherzo movement of Beethoven’s 9th Symphony. We will conclude with an interesting open problem involving objects called bracelets.
Monday, April 16, 2012. Master’s Thesis Defense.
Trevor Vadas, UMaine Master’s candidate in Mathematics (Advisor: Bray).
“Ergodic transformations and measurable sets”
2:10 pm – 3:00 pm, 421 Neville Hall.
Wednesday, April 11, 2012. Master’s Thesis Defense.
Emily Igo, UMaine Master’s candidate in Mathematics (Advisors: Ozluk, Knightly).
“On the Algebraic Reformulation of the Partition Function.”
3:10 pm – 4:00 pm, 108 Neville Hall.
The partition function p(n) is the number partitions of n, i.e. the number of ways to represent n as a nondecreasing sum of positive integers. It has interested mathematicians dating back to Euler in the 1700s. After defining the partition function and looking at some simple examples, there will be a brief look at historical attempts to calculate the value for large integers. Several key results will also be explored, such as the reformulation to an explicit representation as an infinite series and the arithmetic reformulation into a finite sum. There will also be a discussion of the newest result in the field of partition theory due to Ono and Bruinier, the algebraic reformulation, and a detailed sample computation.
Thursday, April 5, 2012
Eisso Atzema, UMaine Mathematics.
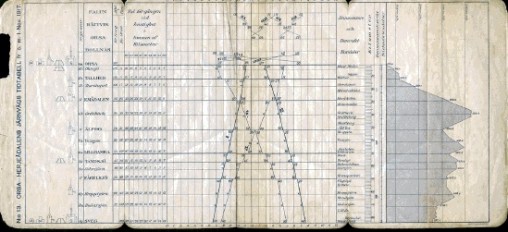
“Lessons on Train Schedules: From String Charts to Teaching Tools.”
11:30 am – 12:30 pm, 421 Neville Hall.
Pizza at 11:30, Talk 11:50-12:30.
The early 20th-century was a time of major reforms in the teaching of mathematics all across the Western world. Among the many changes that were adopted was an increased emphasis on the use of the function concept in its various representations (sounds familiar?). In particular, in a very short time span, graphical illustrations of functions became commonplace in mathematics textbooks.
In this presentation, I will talk about the inclusion of so-called graphical railroad time tables (see figure above) as an example of such a graphical illustration. Among other things, I will discuss the origins of this real-life application of mathematics, its actual use, and how its inclusion in the textbooks evolved over time.
Thursday, December 1, 2011
Arielle Saiber, Associate Professor of Italian, Bowdoin College.
“Niccolo’ Tartaglia’s Poetic Solution to the Cubic Equation”
3:30 pm – 4:30 pm, 421 Neville Hall.
Niccol Fontana’s (known as Niccol Tartaglia, c.1499-1557) famous solution to the cubic equation, which renowned mathematician Girolamo Cardano desperately wanted, got, and published much to Tartaglia’s chagrin, led to one of the first intellectual property cases in Western history. A fascinating element in this sensational ordeal was Tartaglia’s choice to weave his prized solution into a poem. This poem reveals much about Tartaglia’s thoughts on the role of language and the literary arts in the doing of mathematics, and it poses larger questions as to the intersections between mathematics and literature in the Renaissance.
Lecture co-sponsored by Phi Beta Kappa and the School of Computing and Information Science.
Thursday, December 1, 2011. Master’s Thesis Defense, Advisor: Prof. Hiebeler.
Isaac Michaud, Master’s Candidate, Mathematics & Statistics.
“Targeted Treatment in a Community Model”
9:00 am – 9:50 am, 421 Neville Hall.
One of the tenets of integrated pest management is reduction of pesticide use in order to protect human health, the environment and the sustainability of agriculture. An SIS epidemiological community model is analyzed to study how redistributing pesticides among agri- cultural fields can increase pesticide efficacy. We model the spread of a pest from plant to plant like an infection through a population. The population of plants is partitioned into fields called communities where the pest can spread quickly and slowly jump from one commu- nity to another. Each community receives treatment (pesticide) which removes the pest. Instead of uniformly treating every community, we investigate targeted treatment where highly infected communities pro- portionally receive more treatment. The purpose of targeting is that the efficacy of treatment can be increased by applying it to where it is most needed. Using analysis and computer simulation we show that although the endemic density of pests does not change after targeting is implemented, it slows the population’s overall infection rate. Also, targeted treatment increases the likelihood of the pest population dying out due to random fluctuations when pest densities are low.
Thursday, November 17, 2011
Trevor Vadas, Master’s Student, Univ. of Maine Mathematics.
“Irrational Rotations and Invariant Sets”
3:30 pm – 4:30 pm, 108 Neville Hall.
Invariant sets of the unit circle under the action of a rational rotation can have measure zero, full measure, or any number between. However, for irrational rotations, the story is quite different. A classical result, usually proved using some measure ideas and Fourier analysis, states that an invariant set under an irrational rotation has either measure zero or full measure, i.e., irrational rotations are ergodic. Based on recent work of Nillsen, we will discuss a different approach to this problem based on more elementary ideas (outer measure) which provides motivation to Caratheodory’s definition of a measurable set.
Thursday, November 3, 2011
Emily Igo, Master’s Student, Univ. of Maine Mathematics.
“An introduction to Partition Theory”
3:30 pm – 4:30 pm, 108 Neville Hall.
It has been a long-standing problem of interest in number theory to consider the number of partitions of an integer. This same problem has intrigued physicists, as partition theory has direct applications to statistical and quantum physics. First we consider the question, Which is easier to count, ordered partitions or unordered partitions? After handling the simpler case, we will overview some historical methods used to compute p(n), from Euler’s recursion to Hardy and Ramanujan’s asymptotic formula, through Rademacher’s infinite sum. Some special cases will be considered, such as restricting the largest part, and outlines of derivations given, particularly relating to formal power series. Finally, we will see a brief introduction to a new result in the field due to Ken Ono.
Thursday, October 27, 2011
Prof. Ali Abedi, UMaine Dept. of Electrical and Computer Engineering.
“Smart Battery-Free Wireless Sensing”
2:30 pm – 3:30 pm, 100 Neville Hall.
Battery-free wireless sensors developed at the University of Maine under a cooperative agreement with NASA enable a myriad of applications ranging from structural health monitoring to biomedical and space explorations to name a few. Embedding these sensors in structures without the need for changing batteries, their rugged design to withstand harsh environments, and coded communication with multiple access features makes this new technology a desirable candidate for a variety of aerospace and civil infrastructure monitoring applications. This talk presents mathematical theories behind sensor design, communication schemes, and multi tier networking strategies developed to deliver a reliable wireless sensor system.
 |
This is a large scale (42 ft diameter torus) inflatable lunar habitat structure that is built by NASA and instrumented by UMaine Wireless Sensors to make a unique test-bed for technology demonstration. Various aspects of this system including distributed sensing and coding, throughput optimization, channel estimation error analysis, signal detection in presence of interference, two tiered networking, turbo coding and decoding in distributed sensor networks, cooperative relaying methods, and impact localization are presented in this talk. |
Thursday, October 20, 2011
Dr. Jonathan Farley, UMaine Dept. of Computer Science.
“The Most Embarrassing Inequality of My Life”
Matchings in the Permutation Lattice
3:30 pm – 4:30 pm, 421 Neville Hall.
“Can you do it?”
In the spring of 1997, Anders Björner, a visitor at Berkeley’s Mathematical Sciences Research Institute, sent me a handwritten note in response to a question I had asked him. He wanted to know if I could prove, combinatorially, for an n-element poset of height r, that hk≥hn-1-k when k < (n-1)/2. I had been hunting this inequality for perhaps the previous four or five years. I believed that any fact about ordered sets, except artificially-rigged statements, must be provable by order-theoretic means. To my embarrassment, however, I could not deduce this inequality combinatorially. Nor could I concede defeat.
Perhaps I should explain.
Let Sn be the symmetric group on n letters with the weak Bruhat order, which means the following: Write each σ in Sn in the one-line notation σ = σ1…σn. We call (σi,σj) an inversion if i<j but σi>σj. The relation σ≤τ holds if and only if every inversion of σ is an inversion of τ; it turns out this makes Sn into a lattice ― in fact, a very special kind of lattice, one which is “bounded” in the sense of McKenzie.
We say a number i is a descent of σ if σi > σi+1; ascents are defined similarly. For fixed n, let Jk be the set of all permutations with exactly k descents, and let Mk be the set of all permutations with exactly k ascents. The covering relation in Sn with the weak order is given by: σ is a lower cover of τ if you can obtain τ from σ by taking exactly one ascent and reversing the corresponding two letters, turning them into a descent.
Label an n-element poset P with the numbers 1 through n so that 123…n is a linear extension, that is, label P with the numbers 1, 2, 3, up to n so that, whenever an element p is below an element q in the poset, the label of p (a natural number) is less than the label of q. This is called a natural labeling. Let hj be the number of linear extensions of P ― that is, the permutations such that, if p is less than q in the poset, then the label for p appears to the left of the label for q in the permutation―with j descents.
For instance, if P is the four-element zig-zag or fence, one gets (1,3,1) for the h-vector; if P is a five-element antichain, one gets the famous eulerian numbers (1,26,66,26,1).
I could answer Björner’s question if, for n≥3 and 2 ≤ k< n/2-1, I could find an explicit bijection G from Jk to Mk such that for all σ in Jk, σ≤G(σ). Edelman and Reiner found an argument for k=1 and general n in response to a question of mine.
After I gave a talk on this topic at the University of Maine, while flying back to Austria I had an idea.
Tuesday, September 27, 2011
Kevin Roberge, UMaine Mathematics instructor and grad student of Physics.
“Twisted Mathematics: Rubik’s Cube”
12:30 pm – 1:20 pm, 421 Neville Hall.
Rubik’s cube and the many other twisty puzzles that have been created embody a beautiful part of mathematics known as group theory. These hand held puzzles invite problem solvers from all walks of life to enjoy the clearly stated challenge of each puzzle: return to a state of order.
In this discussion Kevin Roberge, a long time fan of twisty puzzles, will introduce some history, mathematics and future of Rubik’s cube and twisty puzzles. He’ll have his modest collection with him and will discuss some of the challenges in solving the puzzles and in creating new puzzles.