Areas of Research
The Stechlinski Lab is focused on solving problems from areas the life sciences and engineering that exhibit a mixture of continuous and discrete dynamics. We investigate these phenomena using nonsmooth analysis, hybrid systems theory, and control and optimization. Examples of recent and ongoing efforts are outlined below.
Hybrid Dynamical Systems
Hybrid systems are a modeling paradigm characterized by a mixture of continuous and discrete behavior. This broad class of systems includes a number of frameworks, such as switching systems, hybrid automata and complementarity systems. Generally, the more abstract the framework, the more widely applicable it is, but the more challenging it is to analyze (due to, e.g., challenges in accurate simulation and solutions exhibiting pathological behavior). We are broadly interested in analyzing hybrid models, with a focus on establishing foundational theory for use in solving control and optimization problems. This includes investigating well-posedness questions (e.g., existence and uniqueness of solutions), as well as qualitative behavior of solutions (e.g., stability and sensitivity theory).
Generalized derivatives theory
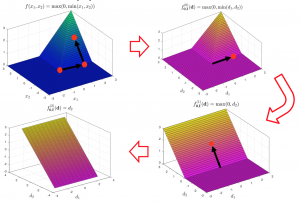
We are interested in making contributions to the theory of generalized derivatives, which extends the classical derivative. Certain classes of generalized derivatives can be supplied to dedicated nonsmooth numerical methods (e.g. equation-solving and optimization) with attractive convergence properties. However, there are a number of hurdles in calculating generalized derivatives in an accurate and automatable way. For example, it is often the case that generalized derivatives do not satisfy sharp calculus rules. Investigating these types of problems in nonsmooth analysis, with computational relevancy in mind, is the main focus here.
Relevant works:
- P. Stechlinski, J. Jäschke, P.I. Barton. Generalized sensitivity analysis of nonlinear programs using a sequence of quadratic programs, Optimization (2019) [Link]
- J. Choi, Theory of lexicographic differentiation in the Banach space setting, MA Thesis (2019) [Link]
- P.I. Barton, K.A. Khan, P. Stechlinski, H.A.J. Watson. Computationally relevant generalized derivatives: theory, evaluation and application, Optimization Methods and Software (2018) [Link]
- P. Stechlinski, K.A. Khan, P.I. Barton. Generalized sensitivity analysis of nonlinear programs, SIAM Journal on Optimization (2018) [Link]
Nonsmooth dynamical systems
A wide range of problems in dynamic simulation and optimization involve functions that are nonsmooth. This lack of differentiability can be problematic in standard theoretical and computational tools. In the models, such nonsmoothness can appear in the right-hand side functions in governing equations or because of embedded optimization problems. We aim to establish foundational theory for these frameworks that mirrors classical theory and is computationally relevant for use in solving practical control and optimization problems.
Relevant works:
- P. Stechlinski. Theory of index-one complementarity systems. Journal of Differential Equations (2021) [Link]
- P. Stechlinski. Optimization-constrained differential equations with active set changes. Journal of Optimization Theory and Applications (2020) [Link]
- P. Stechlinski and P.I. Barton. Dependence of solutions of nonsmooth differential-algebraic equations on parameters, Journal of Differential Equations (2017) [Link]
- P. Stechlinski and P.I. Barton. Generalized derivatives of differential-algebraic equations, Journal of Optimization Theory and Applications (2016) [Link]
Control theory for nonlinear and nonsmooth systems
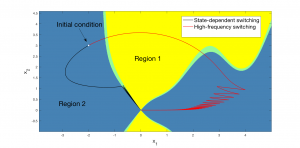In many of the applications of interest, it is of interest to design control strategies to achieve certain performance outcomes (e.g., stabilization, synchronization, robustness to uncertainty, maximization of system metrics). This area of work is motivated to solve control problems in hybrid and nonsmooth systems. This includes optimal control problems involving nonsmooth dynamical systems and hybrid/switching control applied to nonlinear but smooth systems.
Relevant works:
- X.Z. Liu and P. Stechlinski. Switching and impulsive control algorithms for nonlinear hybrid dynamical systems, Nonlinear Analysis: Hybrid Systems (2018) [Link]
- P. Stechlinski and P.I. Barton. Generalized derivatives of optimal control problems with nonsmooth differential-algebraic equations embedded, In: Proceedings 55th IEEE Conference on Decision and Control (2016) [Link]
- X.Z. Liu and P. Stechlinski. Hybrid stabilization and synchronization of nonlinear systems with unbounded delays, Applied Mathematical Modelling (2016) [Link]
- X.Z. Liu and P. Stechlinski. Hybrid control of impulsive systems with distributed delays, Nonlinear Analysis: Hybrid Systems (2014) [Link]
Applications in Mathematical Biology and Engineering
The goal of this research is to analyze applications found in the life sciences and engineering that exhibit hybrid behavior. Examples in mathematical biology include modeling the spread of infectious diseases, social contagions, neural networks, chronic diseases, and opioid abuse in a population, among others. Hybrid and switching behavior is also prevalent in a wide range of engineering problems, such as those found in process systems engineering and power systems. A major focus of this work involves investigating the models in order to predict changes in patterns, estimate important measures, and determine efficient control strategies while minimizing negative effects. Since standard theory in the smooth setting is typically inadequate or unavailable in the hybrid/nonsmooth setting, the tools and methods developed above are applied to these practical problems.
Infectious and chronic diseases
Seasonal fluctuations and shifts in population behavior play an important role in the dynamics of infectious disease epidemics. Examples include a higher transmission of vector-borne diseases during periods of high temperature; dramatic shifts in mosquito birth rates from dry seasons to rainy seasons; regular (and irregular) school closures; and humans altering their behavior given knowledge of an impending or ongoing outbreak. Chronic diseases may similarly exhibit continuous/discrete dynamics. For example, a typical glucose-insulin response involves a biochemical switch. In these cases, hybrid frameworks are appropriate for modeling these phenomena and allow for application of hybrid systems theory.
Relevant works:
- M. Ackley and P. Stechlinski. Lexicographic derivatives of nonsmooth glucose-insulin kinetics under normal and artificial pancreatic responses, Applied Mathematics and Computation (2021) [Link]
- X.Z. Liu and P. Stechlinski. Switching vaccination schemes for vector-borne diseases with seasonal fluctuations, Journal of Biological Systems (2017) [Link]
- X.Z. Liu and P. Stechlinski. Infectious Disease Modeling: A Hybrid System Approach, In: Springer Series in Nonlinear Systems of Complexity (2017) [Link]
- X.Z. Liu and P. Stechlinski. Application of control strategies to a seasonal model of chikungunya disease, Applied Mathematical Modelling (2015) [Link]
Social contagions
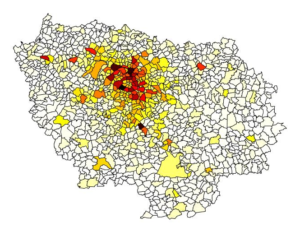
The governing dynamics of certain social behaviors are driven, in part, by bandwagon effects after “tipping point” thresholds are reached, triggering an outburst of activity. For example, this was shown to be the case in the 2005 French riots. In this area of work, we apply theoretical and numerical tools to models of social contagions (e.g., rioting behavior, the opioid epidemic) in order to identify the most influential mechanisms driving these models, with the hope of determining policy considerations to lessen social harm.
Relevant works:
- M. Ackley and P. Stechlinski. Determining key parameters in riots using lexicographic directional differentiation, SIAM Journal on Applied Mathematics (2021) [Link]
- C. Butler. A mathematical model of the opioid epidemic in the state of Maine, Honors Thesis (2020) [Link]
Process and power engineering
A variety of systems in engineering involve continuous but nonsmooth behavior. Examples are found in pharmaceutical manufacturing, multistream heat exchange, bioprocessing, and power/energy systems, due to the presence of thermodynamic phase changes, start-up/shut-down procedures, safety instrumentation, nonsmooth/discontinuous input profiles, etc. In this work, we identify, model, and analyze practical problems from these areas of engineering, which are currently theoretically and/or computationally inaccessible, for design and optimization purposes.
Relevant works:
- S.A. Eisa and P. Stechlinski. Sensitivity analysis of nonsmooth power control systems with an example of wind turbines, Communications in Nonlinear Science and Numerical Simulation (2021) [Link]
- P. Stechlinski, M. Patrascu, P.I. Barton. Nonsmooth DAEs with applications in modeling phase changes, In: Differential-Algebraic Equations Forum (2018) [Link]
- P. Stechlinski and P.I. Barton. Nonsmooth differential-algebraic equations in chemical engineering, Computers & Chemical Engineering (2018) [Link]